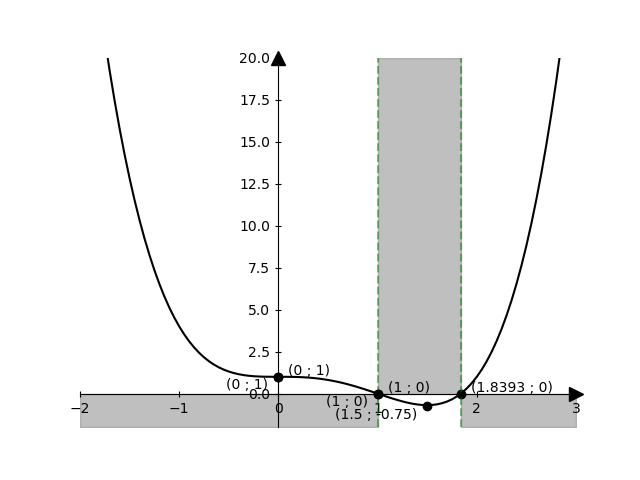
Studio di funzione

Funzione polinomiale

$\displaystyle f(x) = x^4 - 2 x^3 + 1 $

$\forall x \in \mathbb{R}$

Dominio: $\left( - \infty ; + \infty \right)$

$f(-x) = (-x)^4 - 2 (- x) ^3 + 1 = x^4 + 2 x^3 + 1 \ne f(x)$ perciò non è pari

$-f(-x) = - \left( (-x)^4 - 2 (- x) ^3 + 1 \right) = -x^4 - 2 x^3 - 1 \neq f(x)$ perciò non è dispari

Intersezioni con l'asse x (zeri):

$ \left\{ \begin{array}{l} f(x) = 0 \\ f(x) = x^4 - 2 x^3 + 1 \end{array} \right. $

Da cui

$x^4 - 2 x^3 + 1 = 0$

Questo polinomio di IV grado si può scomporre con il metodo di Ruffini. Provando con i divisori del termine noto, si trova che $1$ annulla il polinomio, pertanto esso è divisibile per:

$\displaystyle \left( x - 1 \right) $

Da cui si avrà la seguente divisione di Ruffini:

$ \begin{array}{c|rrrr|r} & 1 & -2 & 0 & 0 & 1 \\ \\ 1 & \downarrow & 1 & -1 & -1 & -1 \\ \hline & 1 & -1 & -1 & -1 & 0 \end{array} $

Da cui si ottiene la seguente scomposizione:

$\displaystyle \left( x - 1 \right) \left( x^3 - x^2 - x - 1 \right) = 0 $

Il polinomio di III grado rimanente non è scomponibile con metodi semplici. Perciò è necessario trovarne gli zeri con il seguente metodo.

$\displaystyle x^3 - x^2 - x - 1 = 0 $

Si calcolino i termini $p$ , $q$ e $\Delta$

$\displaystyle p = - {1 \over 3} \left( {b \over a} \right) ^ 2 + {c \over a} = $

$\displaystyle = - {1 \over 3} \left( { { -1 } \over 1 } \right) ^ 2 + { { -1 } \over 1 } = - { 4 \over 3 } $

$\displaystyle q = {2 \over 27} \left( {b \over a} \right) ^ 3 - {1 \over 3} { {bc} \over {a^2} } + {d \over a} = $

$\displaystyle = {2 \over 27} \left( { { - 1 } \over 1 } \right) ^ 3 - {1 \over 3} { { (-1)(-1)} \over {1^2} } + {{-1} \over 1} = - { 38 \over 27 } $

$\displaystyle \Delta = {{q ^ 2} \over 4} + {{p ^ 3} \over 27} = $

$\displaystyle = {{ \left( - { 38 \over 27 } \right) ^ 2} \over 4} + {{ \left( - { 4 \over 3 } \right) ^ 3} \over 27} = { 1188 \over 2916 } = { 11 \over 27 } $

Siccome $\Delta \gt 0$ avremo 1 radice reale e 2 radici complesse coniugate. Ci interessa solamente la radice reale:

$\displaystyle u = \sqrt[3]{ - { q \over 2} + \sqrt{ \Delta } } = \sqrt[3]{ - { { - { 38 \over 27 } } \over 2} + \sqrt{ { 11 \over 27 } } } = $

$\displaystyle = \sqrt[3]{ { 19 \over 27 } + \sqrt{ 11 \over 27 } } \approx 1.10302 $

$\displaystyle v = \sqrt[3]{ - { q \over 2} - \sqrt{ \Delta } } = \sqrt[3]{ - { { - { 38 \over 27 } } \over 2} - \sqrt{ { 11 \over 27 } } } = $

$\displaystyle = \sqrt[3]{ { 19 \over 27 } - \sqrt{ 11 \over 27 } } \approx 0.40293 $

Da cui si ricava infine:

$\displaystyle x_r = u + v - { b \over {3a} } = 1.10302 + 0.40293 - { { -1 } \over {3 \cdot 1} } \approx 1.83929 \approx 1.84 $

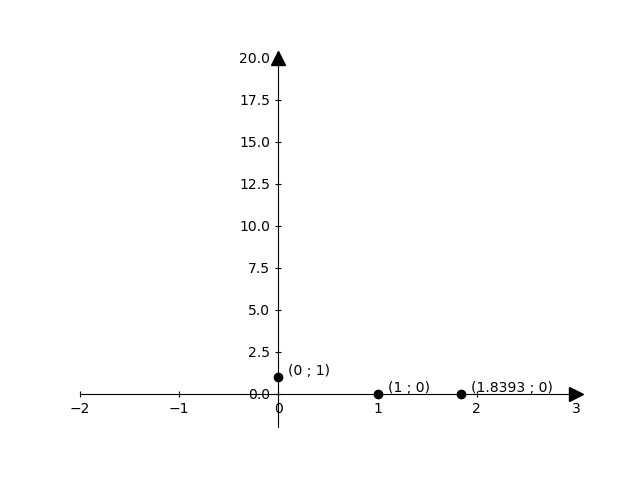
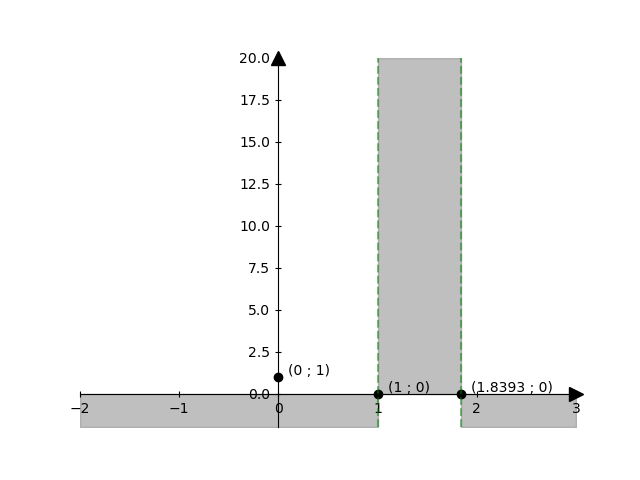
Intersezioni asse x: $( 1 ; 0 )$ e $( 1.84 ; 0 )$

Intersezioni con l'asse y:

$ \left\{ \begin{array}{l} x = 0 \\ f(x) = x^4 - 2 x^3 + 1 \end{array} \right. $

Da cui

$f(0) = (0)^4 - 2 (0)^3 + 1 = 1$

Intersezioni asse y: $( 0 ; 1 )$

$Intersec_xy$

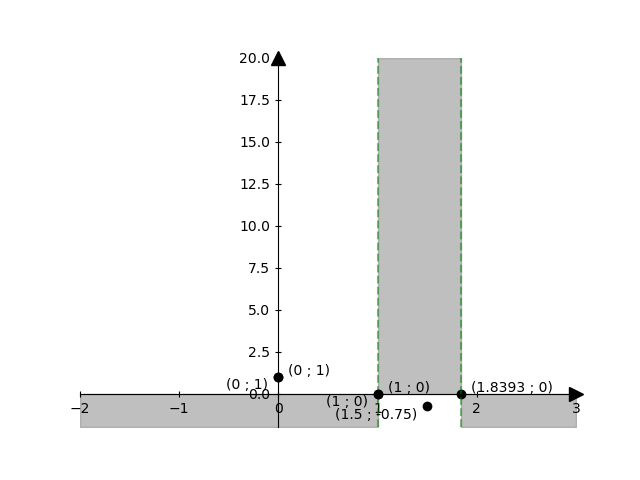
$y \gt 0$ quindi $x^4 - 2 x^3 + 1 \gt 0$

Ovvero, utilizzando la forma scomposta ricavata in precedenza:

$\displaystyle \left( x - 1 \right) \left( x^3 - x^2 - x - 1 \right) \gt 0 $

Dal primo fattore

$\displaystyle \left( x - 1 \right) \gt 0 $

Si ha

$\displaystyle x \gt 1 $

Del secondo fattore

$\displaystyle \left( x^3 - x^2 - x - 1 \right) \gt 0 $

Sappiamo che interseca l'asse x in un solo punto ( x = 1.84 ). Provando a sostituire valori di x inferiori (per esempio 0), si ottengono valori negativi, mentre per valori di x superiori (per esempio 2) si ottengono valori positivi. Pertanto si ha:

$\displaystyle x \gt 1.84 $

Combinando graficamente le due condizioni:

             1      1.84
     --------|+++++++|+++++++
     --------|-------|+++++++
        +    |   -   |   +

$func_sign$

$\displaystyle \lim_{ x \to - \infty} { x^4 - 2 x^3 + 1 } = + \infty $

Possibile asintoto obliquo

$\displaystyle m_1 = \lim_{ x \to - \infty} { { f(x) } \over x } = \lim_{ x \to - \infty} { { x^4 - 2 x^3 + 1 } \over x } = \left[ { { \infty } \over { \infty } } \right] = - \infty $

Non c'è asintoto obliquo per $x \to - \infty$

$\displaystyle \lim_{ x \to + \infty} { x^4 - 2 x^3 + 1 } = \left[ + \infty - \infty \right] = + \infty $

Con calcoli analoghi al limite precedente si dimostra che non c'è asintoto obliquo per $x \to + \infty$

$ y'= 4 x^3 - 6 x^2 $

$\displaystyle \left\{ \begin{array}{l} y' = 0 \\ y'= 4 x^3 - 6 x^2 \end{array} \right. $

Da cui

$\displaystyle 4 x^3 - 6 x^2 = 0 $

Scomponendo il polinomio si ha:

$\displaystyle 2 x^2 \left( 2x - 3 \right) = 0 $

Che si annulla quando:

$\displaystyle 2 x^2 = 0 $

$\displaystyle x = 0 $

Oppure quando:

$\displaystyle 2x - 3 = 0 $

$\displaystyle x = { 3 \over 2 } $

$y' \gt 0$ quindi $4 x^3 - 6 x^2 \gt 0$

Ovvero, usando la forma scomposta:

$\displaystyle 2 x^2 \left( 2x - 3 \right) \gt 0 $

Dal primo fattore

$\displaystyle 2 x^2 \gt 0 $

$\displaystyle \forall x \ne 0 $

Dal secondo fattore

$\displaystyle 2x - 3 \gt 0 $

$\displaystyle x \gt { 3 \over 2 } $

Combinando graficamente le due condizioni:

             0      3/2
     ++++++++|+++++++|+++++++
     --------|-------|+++++++
        -    |   -   |   +   
       Dec.     Dec.    Cres.

Si ricavino:

$\displaystyle f(0) = 0^4 - 2 (0)^3 + 1 = 1 $

$\displaystyle f(3/2) = (3/2)^4 - 2 (3/2)^3 + 1 = - 12/16 = - 3/4 $

Da ciò si ha che:

$\left( 0 ; 1 \right)$ è un flesso orizzontale

$\left( 3/2 ; - 3/4 \right)$ è un minimo

$\displaystyle y''= 12 x^2 - 12 x $

$ \left\{ \begin{array}{l} y'' = 0 \\ y''= 12 x^2 - 12 x \end{array} \right. $

Da cui

$\displaystyle 12 x^2 - 12 x = 0 $

Si può scomporre:

$\displaystyle 12 x \left( x - 1 \right) = 0 $

Che si annulla quando:

$\displaystyle 12 x = 0 $

$\displaystyle x = 0 $

Oppure quando:

$\displaystyle x - 1 = 0 $

$\displaystyle x = 1 $

$y'' \gt 0$ quindi $12 x^2 - 12 x \gt 0$

Ovvero, usando la forma scomposta:

$\displaystyle 12 x \left( x - 1 \right) \gt 0 $

Dal primo fattore:

$\displaystyle 12 x \gt 0 $

$\displaystyle x \gt 0 $

Dal secondo fattore:

$\displaystyle x - 1 \gt 0 $

$\displaystyle x \gt 1 $

Combinando graficamente le due condizioni:

             0       1
     --------|+++++++|+++++++
     --------|-------|+++++++
        +    |   -   |   +
        Up      Down     Up

Si ricavino:

$\displaystyle f(0) = 0^4 - 2 (0)^3 + 1 = 1 $

$\displaystyle f(1) = (1)^4 - 2 (1)^3 + 1 = 0 $

Da ciò si ha che:

$\left( 0 ; 1 \right)$ si conferma essere un flesso orizzontale

$\left( 1 ; 0 \right)$ è un flesso obliquo

$func_minmaxflex$

$func$