Studio di funzione

Funzione con frazione algebrica

$\displaystyle y= { {2x + 1} \over { x^2 - 2x + 1 } } $

Poichè compare un denominatore:

$\displaystyle x^2 - 2x + 1 \neq 0 $

Da cui:

$\displaystyle \left( x - 1 \right) ^2 \neq 0 $

$\displaystyle x \neq 1 $

Dominio:

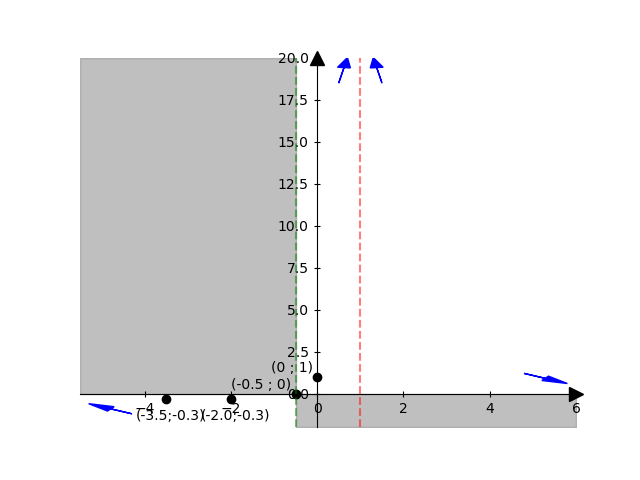
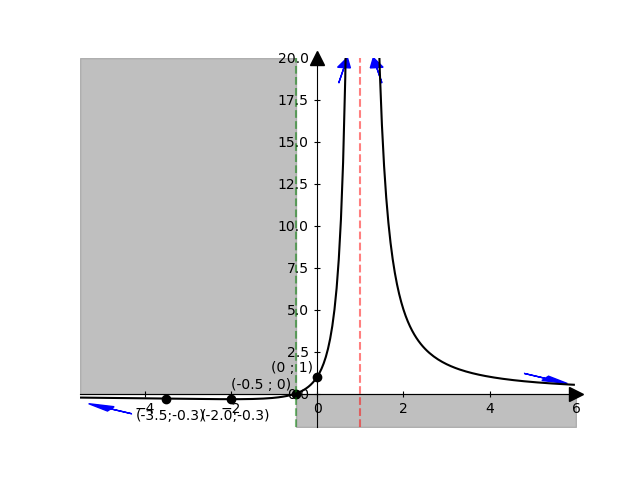
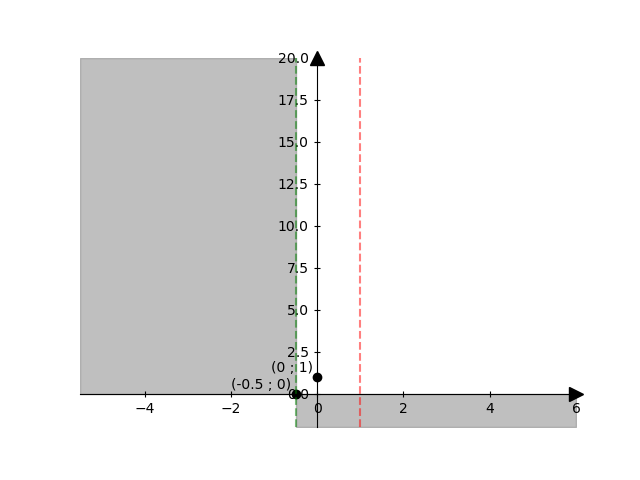
$\displaystyle \left( - \infty ; 1 \right) \cup \left( 1 ; + \infty \right) $

$Domain$

$\displaystyle f(-x) = { {2(-x) + 1} \over { (-x)^2 - 2(-x) + 1 } } \neq f(x) $

Non è pari

$\displaystyle -f(-x) = - { {2(-x) + 1} \over { (-x)^2 - 2(-x) + 1 } } \neq f(x) $

Non è dispari

Intersezioni con l'asse x (zeri):

$\displaystyle \left\{ \begin{array}{l} y = 0 \\ y= { {2x + 1} \over { x^2 - 2x + 1 } } \end{array} \right. $

Da cui

$\displaystyle { {2x + 1} \over { x^2 - 2x + 1 } } = 0 $

Solo il numeratore può diventare nullo, pertanto:

$\displaystyle 2x + 1 = 0 $

$\displaystyle x = - { 1 \over 2 } $

Intersezioni asse x: $( - { 1 \over 2 } ; 0 )$

Intersezioni con l'asse y:

$\displaystyle \left\{ \begin{array}{l} x = 0 \\ y= { {2x + 1} \over { x^2 - 2x + 1 } } \end{array} \right. $

Da cui

$\displaystyle y(0)= { {2(0) + 1} \over { (0)^2 - 2(0) + 1 } } = 1 $

Intersezioni asse y: $( 0 ; 1 )$

$intersec_xy$

$y \gt 0$ quindi

$\displaystyle { {2x + 1} \over { x^2 - 2x + 1 } } \gt 0 $

Si studiano separatamente numeratore e denominatore:

$\displaystyle {2x + 1} \gt 0 \Rightarrow x \gt -{1 \over 2} $

$\displaystyle x^2 - 2x + 1 \gt 0 \Rightarrow \left( x - 1 \right) ^2 \gt 0 \Rightarrow \forall x \ne 1 $

           -1/2      1
     --------|+++++++|+++++++
     ++++++++|+++++++o+++++++
        -    |   +   |   +

$func_sign$

$\displaystyle \lim_{ x \to - \infty} { {2x + 1} \over { x^2 - 2x + 1 } } = \left[ {-\infty} \over {+\infty} \right] = $

$\displaystyle = \lim_{ x \to - \infty} { { x \left( 2 + 1/x \right) } \over { x^2 \left( 1 - 2/x + 1/x^2 \right) } }= { 2 \over - \infty } = 0^- $

Asintoto orizzontale di equazione $y = 0$

$\displaystyle \lim_{ x \to 1^-} { {2x + 1} \over { x^2 - 2x + 1 } } = { 3 \over {0^+} } = +\infty $

Asintoto verticale di equazione $x = 1$

$\displaystyle \lim_{ x \to 1^+} { {2x + 1} \over { x^2 - 2x + 1 } } = { 3 \over {0^+} } = +\infty $

Asintoto verticale di equazione $x = 1$

$\displaystyle \lim_{ x \to + \infty} { {2x + 1} \over { x^2 - 2x + 1 } } = \left[ {+\infty} \over {+\infty} \right] = $

$\displaystyle = \lim_{ x \to - \infty} { { x \left( 2 + 1/x \right) } \over { x^2 \left( 1 - 2/x + 1/x^2 \right) } }= { 2 \over + \infty } = 0^+ $

Asintoto orizzontale di equazione $y = 0$

$func_limits$

$\displaystyle y'= { { \left( 2 \right) \left( x^2 - 2x + 1 \right) - \left( 2x +1 \right) \left( 2x - 2 \right) } \over { \left( x^2 - 2x + 1 \right)^2 } } = $

$\displaystyle = { { 2 x^2 - 4x + 2 - 4x^2 -2x + 4x + 2 } \over { \left( x - 1 \right)^4 } } = { { - 2 x^2 - 2x + 4 } \over { \left( x - 1 \right)^4 } } = $

$\displaystyle = { { -2 \left( x^2 + x -2 \right) } \over { \left( x - 1 \right)^4 } } = { { - 2 \left( x - 1 \right) \left( x + 2 \right) } \over { \left( x - 1 \right)^4 } } = $

$\displaystyle = { { - 2 \left( x + 2 \right) } \over { \left( x - 1 \right)^3 } } $

$\displaystyle \left\{ \begin{array}{l} y' = 0 \\ y'= { { - 2 \left( x + 2 \right) } \over { \left( x - 1 \right)^3 } } \end{array} \right. $

Da cui

$\displaystyle { { - 2 \left( x + 2 \right) } \over { \left( x - 1 \right)^3 } } = 0 $

Solo il numeratore può diventare nullo, pertanto:

$\displaystyle { - 2 \left( x + 2 \right) } = 0 $

$\displaystyle x + 2 = 0 $

$\displaystyle x = -2 $

$y' \gt 0$ quindi

$\displaystyle { { - 2 \left( x + 2 \right) } \over { \left( x - 1 \right)^3 } } \gt 0 $

Bisogna studiare separatamente numeratore e denominatore e combinare insieme i segni:

$\displaystyle { - 2 \left( x + 2 \right) } \gt 0 $

$\displaystyle x \lt - 2 $

$\displaystyle \left( x - 1 \right)^3 \gt 0 $

$\displaystyle x \gt 1 $

Combinando graficamente le due condizioni:

           -2       1
     +++++++|-------|-------
     -------|-------|+++++++
        -   |   +   |   - 
       Dec.   Cres.   Dec.

Si ricavi:

$\displaystyle f(-2) = { {2 (-2) + 1} \over { (-2)^2 - 2(-2) + 1 } } = - { 1 \over 3 } $

Da ciò si ha che:

$\left( -2 ; - { 1 \over 3 } \right)$ è un minimo.

$\displaystyle y''= -2 { { \left( 1 \right) \left( x - 1 \right) ^3 - \left( x + 2 \right) 3 \left( x - 1 \right) ^2 } \over { \left( x - 1 \right) ^6 } } = $

$\displaystyle = -2 { { \left( x - 1 \right) - 3 \left( x + 2 \right) } \over { \left( x - 1 \right) ^4 } } = $

$\displaystyle = { { 4x + 14 } \over { \left( x - 1 \right) ^4 } } $

$\displaystyle \left\{ \begin{array}{l} y'' = 0 \\ y''= { { 4x + 14 } \over { \left( x - 1 \right) ^4 } } \end{array} \right. $

Da cui

$\displaystyle { { 4x + 14 } \over { \left( x - 1 \right) ^4 } } = 0 $

$\displaystyle 4x + 14 = 0 $

$\displaystyle x = - { 14 \over 4 } = - { 7 \over 2 } $

$y'' \gt 0$ quindi:

$\displaystyle { { 4x + 14 } \over { \left( x - 1 \right) ^4 } } \gt 0 $

Bisogna studiare il segno dei termini separatamente e combinarli insieme:

$\displaystyle 4x + 14 \gt 0 $

$\displaystyle x \gt - { 7 \over 2} $

$\displaystyle \left( x - 1 \right) ^4 \gt 0 $

$\displaystyle \forall x \ne 1 $

Combinando graficamente le due condizioni:

          -7/2      1 
     -------|+++++++|+++++++
     +++++++|+++++++o+++++++
        -   |   +   |   +
       Down    Up      Up

Si ricavi:

$\displaystyle f\left(-{ 7 \over 2} \right) = { {2 \left( - { 7 \over 2} \right) + 1} \over { \left( - { 7 \over 2} \right)^2 - 2\left( - { 7 \over 2} \right) + 1 } } = - { 8 \over 27 } $

Si ha quindi che:

$\left( - 7/2 ; - 8/27 \right)$ è un flesso obliquo

$func_minmaxflex$

$func$