Studio di funzione

Funzione con radicali

$\displaystyle y= \sqrt[3]{ 6x - x^2 } $

Non ci sono condizioni che limitano il dominio, perciò:

$\forall x \in \mathbb{R}$

$f(-x) = \sqrt[3]{ 6(-x) - (-x)^2 } = \sqrt[3]{ -6x -x^2 } \neq f(x)$ perciò non è pari

$-f(-x) = - \sqrt[3]{ 6(-x) - (-x)^2 } = \sqrt[3]{ 6x + x^2 } \neq f(x)$ perciò non è dispari

Intersezioni con l'asse x (zeri):

$ \left\{ \begin{array}{l} y = 0 \\ y= \sqrt[3]{ 6x - x^2 } \end{array} \right. $

Da cui

$y= \sqrt[3]{ 6x - x^2 } = 0$

$6x - x^2 = 0$

$x \left( 6 - x \right) = 0$

Prima soluzione: $x = 0$

Seconda soluzione $6 - x = 0$ da cui $x = 6$

Intersezioni asse x: $( 0 ; 0 )$ e $( 6 ; 0 )$

Intersezioni con l'asse y:

$ \left\{ \begin{array}{l} x = 0 \\ y= \sqrt[3]{ 6x - x^2 } \end{array} \right. $

Da cui

$y(0) = \sqrt[3]{ 6(0) - (0)x^2 } = 0$

Intersezione con asse y: $( 0 ; 0 )$

$Intersec_xy$

$y \gt 0$ quindi $\sqrt[3]{ 6x - x^2 } \gt 0$

$6x - x^2 \gt 0$

$x \gt 0$

$x \lt 6$

             0       6
     --------|+++++++|+++++++
     ++++++++|+++++++|-------
        -    |   +   |   -

$func_sign$

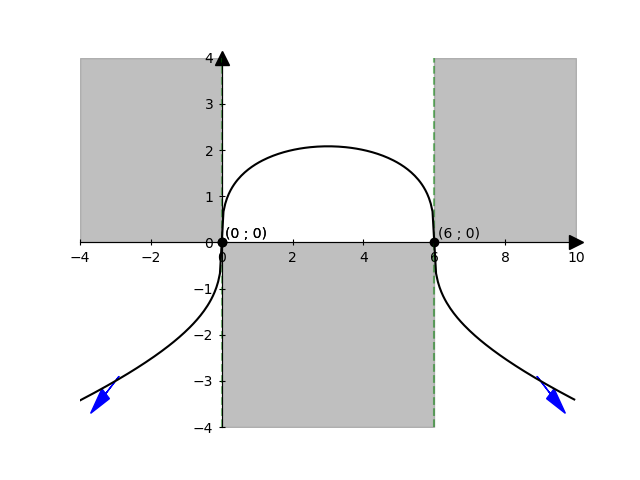
$\displaystyle \lim_{ x \to - \infty} { \sqrt[3]{ 6x - x^2 } } = - \infty $

Possibile asintoto obliquo

$\displaystyle m_1 = \lim_{ x \to - \infty} { { f(x) } \over x } = $

$\displaystyle = \lim_{ x \to - \infty} { { \sqrt[3]{ 6x - x^2 } } \over x } = \left[ {- \infty } \over {- \infty } \right] = $

Applicando de l'Hopital:

$\displaystyle = \lim_{ x \to - \infty} { {1 \over 3} { { 6 - 2x } \over { \sqrt[3]{ \left( 6x - x^2 \right) ^2 } } } \cdot { 1 \over 1} } = \left[ { \infty } \over {\infty } \right] = $

E fattorizzando $x$ a numeratore e denominatore:

$\displaystyle = \lim_{ x \to - \infty} { {1 \over 3} { { x \left( { 6 \over x } - 2 \right) } \over { x^{4 / 3} \sqrt[3]{ \left( {6 \over x} - 1 \right) ^ 2 } } } } = $

$\displaystyle = \lim_{ x \to - \infty} { {1 \over 3} { { \left( { 6 \over x } - 2 \right) } \over { x^{ 1 / 3} \sqrt[3]{ \left( {6 \over x} - 1 \right) ^ 2 } } } } = { { -2 } \over { - \infty } } = 0 $

Per avere asisntoto obliquo $m_1 \ne 0$, pertanto non c'è asintoto obliquio sinistro e non è necessario calcolare:

$\displaystyle q_1 = \lim_{ x \to - \infty} { { f(x) } - m_1 x } $

$\displaystyle \lim_{ x \to + \infty} { \sqrt[3]{ 6x - x^2 } } = { \sqrt[3]{ \left[ \infty - \infty \right] } } = $

$\displaystyle = \lim_{ x \to + \infty} { \sqrt[3]{ x^2 \left( {6 \over x} - 1 \right) } } = - \infty $

Possibile asintoto obliquo

$\displaystyle m_2 = \lim_{ x \to + \infty} { { f(x) } \over x } = $

$\displaystyle = \lim_{ x \to + \infty} { { \sqrt[3]{ 6x - x^2 } } \over x } = \left[ {+ \infty } \over {+ \infty } \right] = $

Con passaggi analoghi al caso precedente si ha che:

$\displaystyle = \lim_{ x \to + \infty} { {1 \over 3} { { \left( { 6 \over x } - 2 \right) } \over { x^{ 1 / 3} \sqrt[3]{ \left( {6 \over x} - 1 \right) ^ 2 } } } } = { { -2 } \over { + \infty } } = 0 $

Per avere asisntoto obliquo $m_2 \ne 0$, pertanto non c'è asintoto obliquio destro e non è necessario calcolare:

$\displaystyle q_2 = \lim_{ x \to + \infty} { { f(x) } - m_2 x } $

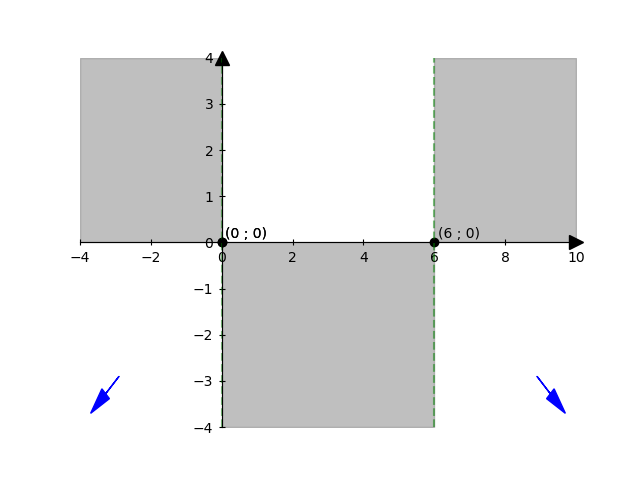
$func_limits$

$\displaystyle y'= { { 1 \over 3 } {1 \over { \left( 6x - x^2 \right) ^{2/3} } } \left( 6 - 2 x \right) } = { { 6 - 2x } \over { 3 \sqrt[3]{ \left( 6x - x^2 \right) ^2 } } } $

$\displaystyle \left\{ \begin{array}{l} y' = 0 \\ y'= { { 6 - 2x } \over { 3 \sqrt[3]{ \left( 6x - x^2 \right) ^2 } } } \end{array} \right. $

Da cui

${ { 6 - 2x } \over { 3 \sqrt[3]{ \left( 6x - x^2 \right) ^2 } } } = 0$

${ 6 - 2x } = 0$

$x = 3$

$y' \gt 0$ quindi ${ { 6 - 2x } \over { 3 \sqrt[3]{ \left( 6x - x^2 \right) ^2 } } } \gt 0$

Bisogna studiare due termini separatamente e combinare insieme i segni:

$6 - 2x \gt 0$ $\Rightarrow x \lt 3$

$3 \sqrt[3]{ \left( 6x - x^2 \right) ^2 } \gt 0$ $\Rightarrow \forall x \neq \pm 3$

           -3       3
     +++++++|+++++++|-------
     +++++++o+++++++o+++++++
        +   |   +   |   -
      Cres.   Cres.    Dec.

$ y''= - {1 \over 3} { { 2 \left( 6x-2 x^2 \right) ^3 + { 2 \over 3 } \left( 6 -2 x \right) ^2 } \over { \left( 6x - 2 x ^2 \right)^5 } } $

TODO

$ \left\{ \begin{array}{l} y'' = 0 \\ y''= - 9 { { \sqrt{ x^2 -9 } } \over { \left( x^2 -9 \right)^2 } } \end{array} \right. $

Da cui

$- 9 { { \sqrt{ x^2 -9 } } \over { \left( x^2 -9 \right)^2 } } = 0$

$\sqrt{ x^2 -9 } = 0$ $\Rightarrow x = \pm 3$

Per $x = \pm 3$ si hanno inversioni di concavità, ma tali punti sono anche estremi del dominio e quindi non sono flessi

$y'' \gt 0$ quindi $- 9 { { \sqrt{ x^2 -9 } } \over { \left( x^2 -9 \right)^2 } } \gt 0$

Bisogna studiare il segno dei termini separatamente e combinarli insieme:

$- 9 \gt 0$ $\Rightarrow \nexists x \in \mathbb{R}$

$\sqrt{ x^2 -9 } \gt 0$ $\Rightarrow x \neq \pm 3$

$\left( x^2 -9 \right)^2 \gt 0$ $\Rightarrow x \neq \pm 3$

            -3       0       3
     --------|-------|-------|-------
     ++++++++o+++++++|+++++++o+++++++
     ++++++++o+++++++|+++++++o+++++++
        -    |       |       |   -
       Down                    Down

$func$