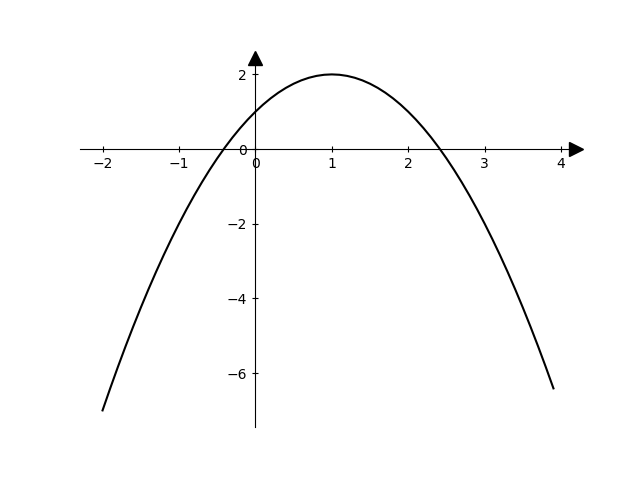
Parabola

Calcolare le proprietà della seguente parabola

$\displaystyle y = - x^2 + 2 x + 1$

Identificati i coefficienti dell'equazione esplicita:

$\displaystyle \begin{array}{l} a = -1 \\ b = 2 \\ c = 1 \end{array}$

Si procede a determinare:

$\displaystyle \Delta = 2^2 - 4 ( -1 ) 1 = 8$

$\displaystyle V = \left( - { 2 \over {-2}} ; - { 8 \over { -4 } } \right) = \left( 1 ; 2 \right)$

$\displaystyle F = \left( - { 2 \over {-2}} ; - { {1 - 8} \over { -4 } } \right) = \left( 1 ; - { 7 \over 4 } \right)$

Intersezione con l'asse delle ordinate:

$\displaystyle y(0) = - 0^2 + 2 \cdot 0 + 1 = 1$

$\displaystyle \left( 0 ; 1 \right)$

Intersezione con l'asse delle ascisse:

$\displaystyle 0 = - x^2 + 2 x + 1$

$\displaystyle x_{1,2} = { { -2 \pm \sqrt{8} } \over { -2 } } = 1 \mp \sqrt{2}$

$\displaystyle \begin{array}{l} x_{1} = 1 - \sqrt{2} \approx -0.41 \\ x_{2} = 1 + \sqrt{2} \approx 2.41 \end{array}$

$\displaystyle \left( -0.41 ; 0 \right)$

$\displaystyle \left( 2.41 ; 0 \right)$

Grafico:

$Grafico$